Arbeitskarten für Schülerinnen und Schüler
Klasse 8 ■ Profilfach Informatik, Mathematik, Physik (IMP) ■ Baden-Württemberg ■ ■ ■

72,00 Euro
inkl. MwSt., zzgl. Versand
108 Arbeitskarten DIN A4 im Ordner
Arbeitskarten Daten und Codierung II
Für die Art, wie Daten gespeichert werden, haben sich Strukturen etabliert – so genannte Datenstrukturen. Die Schülerinnen und Schüler lernen die abstrakt erscheinenden Strukturen Liste, Baum und Graph kennen und entdecken, dass sie sich in zahlreichen Beispielen in unserem Alltag wiederfinden.
Die Graphentheorie ist in der Informatik von großer Bedeutung, um netzartige Strukturen wie Straßen-, Versorgungs- und Computernetze oder soziale Strukturen zu untersuchen. Mit dem so genannten Briefträgerproblem, dem Problem des Handlungsreisenden und dem Problem minimaler Spannbäume lernen die Schülerinnen und Schüler alltagsrelevante Problemstellungen kennen, die mit Hilfe der Graphentheorie gelöst werden können.
Dabei wenden sie mit dem Kruskal-Algorithmus und der Multiple-Fragment-Heuristik zwei Standard-Verfahren der Informatik an.
Mit diesen 9 Themen:
Datenstruktur Liste
Datenstruktur Baum
Datenstruktur Graph
Grundbegriffe zu Graphen
Eulersche Kantenzüge
Königsberger Brückenproblem
Briefträgerproblem
Problem des Handlungsreisenden
Minimaler Spannbaum
Weiterführende Informationen
Welches → Konzept liegt unserem Material für das Fach Informatik 8 im Profilfach Informatik, Mathematik, Physik (IMP) zugrunde?
Wie sind die → Arbeitskarten für Schülerinnen und Schüler aufgebaut?
Lässt sich das Material für den Unterricht in großen Klassen auch → erweitern?
Wie können Sie → Ersatzteile für unser Material für das Fach Informatik (IMP) Klasse 8 bestellen?
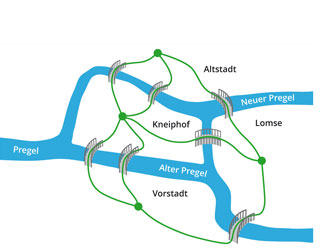
Die Schülerinnen und Schüler lernen das Königsberger Brückenproblem kennen, dessen Lösung durch den Schweizer Mathematiker Leonhard Euler heute als Geburtsstunde der Graphentheorie gilt.
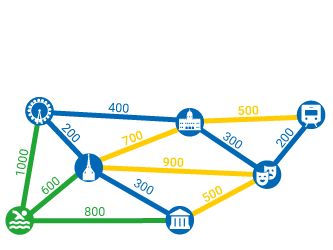
Der minimale Spannbaum ist ein Optimierungsproblem aus der Graphentheorie, das beispielsweise für das Verlegen von Versorgungsleitungen relevant ist. Die Schülerinnen und Schüler lernen, mit Hilfe des Kruskal-Algorithmus minimale Spannbäume zu ermitteln.
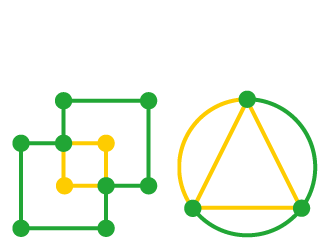
Die Eulerschen Kantenzüge bilden die Grundlage für Optimierungsprobleme der Graphentheorie wie beispielsweise das Briefträgerproblem. Anhand einfacher, anschaulicher Zeichnungen lernen die Schülerinnen und Schüler Eulerwege und Eulerkreise zu erkennen und zu unterscheiden.
Kontakt Impressum AGB Datenschutz
© Copyright Dr. Jörg Kraus − Experimente Materialien Schulungen 2020–2025